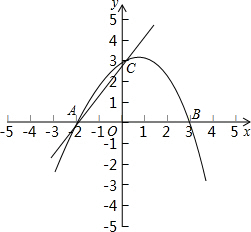问题
解答题
已知抛物线y=ax2+bx+c与x轴交于不同的两点A(x1,0)和B(x2,0)与y轴的正半轴交于点C,如果x1、x2是方程x2-x-6=0的两个根(x1<x2)且△ABC的面积为
(1)求此抛物线解析式; (2)求直线AC的解析式; (3)求直线BC的解析式. |
答案
(1)∵x1、x2是方程x2-x-6=0的两个根(x1<x2)
∴x1=-2,x2=3,
∵△ABC的面积为
,点C位于y轴的正半轴15 2
∴
=5c 2 15 2
∴c=3
∴A,B,C的坐标为(-2,0),(3,0),(0,3)
把(-2,0),(3,0),(0,3)代入y=ax2+bx+c得:
,4a-2b+c=0 9a+3b+c=0 c=3
解得a=- 1 2 b= 1 2 c=3
∴此抛物线解析式为y=-
x2+1 2
x+3;1 2
(2)设直线AC的解析式为y=kx+b
把(-2,0),(0,3)代入y=kx+b得:
,解得-2k+b=0 b=3 k= 3 2 b=3
∴直线AC的解析式为y=
x+3;3 2
(3)同理得:直线BC的解析式为y=-x+3.