问题
解答题
如图，在四边形ABCD中，AB=3cm，CD=2cm，∠BAD=60。，∠CDA=∠CBA=90。，求四边形ABCD的面积。
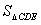
答案
解：延长AD、BC相交于点E，在Rt△ABE中
∵∠A=60。 ∴∠E=30。
又∵EB=AB·tan A ED=DC·cotE
∴EB=3·tan 60。=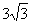
ED=2·cot30。=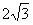 
∴ 
=
-
=
=
=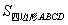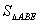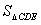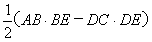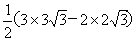