问题
解答题
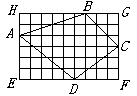
在一个9×6的长方形内，有一个凸四边形(如图)。用毕克定理先求出它的面积来，再用拼割方法计算它的面积，看两者是否一致。
答案
解： ①由毕克定理得：
25+7÷2-1=27.5(面积单位)；
②用拼割方法得：
ABCD的面积=长方形EFGH的面积-四角上的四个三角形的面积
=9×6-(6×2÷2+3×3÷2+4×3÷2+4×5÷2)
=54-(6+4.5+6+10)
=27.5(面积单位)。
搜题请搜索小程序“爱下问搜题”