如图所示,abcd为质量M=2 kg的导轨,放在光滑绝缘的水平面,另有一根质量m=0.6 kg的金属棒PQ平行于bc放在水平导轨上,PQ棒左边靠着绝缘的竖直立柱e、f(竖直立柱光滑,且固定不动),导轨处于匀强磁场中,磁场以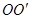 为界,左侧的磁场方向竖直向上,右侧的磁场方向水平向右,磁感应强度大小都为B=0.8 T.导轨的bc段长l=0.5 m,其电阻r=0.4Ω,金属棒的电阻R=0.2Ω,其余电阻均可不计.金属棒与导轨间的动摩擦因数m=0.2.若在导轨上作用一个方向向左、大小为F=2N的水平拉力,设导轨足够长,重力加速度g取
为界,左侧的磁场方向竖直向上,右侧的磁场方向水平向右,磁感应强度大小都为B=0.8 T.导轨的bc段长l=0.5 m,其电阻r=0.4Ω,金属棒的电阻R=0.2Ω,其余电阻均可不计.金属棒与导轨间的动摩擦因数m=0.2.若在导轨上作用一个方向向左、大小为F=2N的水平拉力,设导轨足够长,重力加速度g取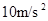 ,试求:
,试求:
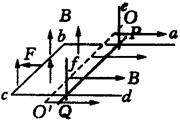
(1)导轨运动的最大加速度;
(2)导轨的最大速度;
(3)定性画出回路中感应电流随时间变化的图线.
(1) (2)
(2)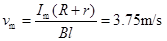 (3)见解析
(3)见解析
解:导轨在外力作用下向左加速运动,由于切割磁感线,在回路中要产生感应电流,导轨的bc边及金属棒PQ均要受到安培力作用,PQ棒受到的支持力要随电流的变化而变化,导轨受到PQ棒的摩擦力也要变化,因此导轨的加速度要发生改变.导轨向左切割磁感线时,有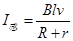 ,① 导轨受到向右的安培力
,① 导轨受到向右的安培力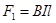 ,金属棒PQ受到向上的安培力
,金属棒PQ受到向上的安培力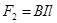 ,导轨受到PQ棒对它的摩擦力
,导轨受到PQ棒对它的摩擦力 ,根据牛顿第二定律,有F-BIl-m(mg-BIl)=Ma,即F-(1-m)BIl-mg=Ma.②
,根据牛顿第二定律,有F-BIl-m(mg-BIl)=Ma,即F-(1-m)BIl-mg=Ma.②
(1)当刚拉动导轨时,v=0,由①式可知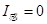 ,则由②式可知,此时有最大加速度
,则由②式可知,此时有最大加速度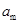 ,即
,即 .
.
(2)随着导轨速度v增大, 增大而a减小,当a=0时,有最大速度
增大而a减小,当a=0时,有最大速度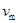 ,从②式可得
,从②式可得 ,有
,有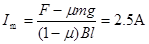 ③ 将
③ 将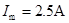 代入①式,得
代入①式,得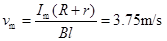 .
.
(3)从刚拉动导轨开始计时,t=0时,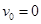 ,I=0,当
,I=0,当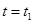 时,v达到最大,I达到2.5 A,电流I随时间t的变化图线如图所示.
时,v达到最大,I达到2.5 A,电流I随时间t的变化图线如图所示.
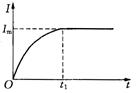
本题考查的是电磁感应定律和力学综合的相关问题,根据电磁感应定律和安培力的计算,利用牛顿第二定律计算出加速度;再根据运动学相关规律计算出最大电流,利用欧姆定律从而计算出导轨的最大速度;最后根据感应电流的变化画出图线;

