(12分) 如图所示,间距l=0.3 m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内.在水平面a1b1b2a2区域内和倾角θ=37°的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4 T,方向竖直向上和B2=1 T、方向垂直于斜面向上的匀强磁场.电阻R=0.3 Ω、质量m1=0.1 kg、长为l的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好.一端系于K杆中点的轻绳平行于导轨绕过轻质定滑轮自然下垂,绳上穿有质量m2=0.05 kg的小环.已知小环以a=6 m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动.不计导轨电阻和滑轮摩擦,绳不可伸长.取g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
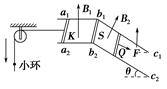
求(1)小环所受摩擦力的大小;
(2)Q杆所受拉力的瞬时功率.
(1)0.2 N (2)2 W
题目分析:(1)以小环为研究对象,在环沿绳下滑过程中,受重力m2g和绳向上的摩擦力f,由牛顿第二定律知m2g-f=m2a.
代入数据解得f=m2(g-a)=0.05×(10-6) N=0.2 N.
(2)根据牛顿第二定律知,小环下滑过程中对绳的反作用力大小f′=f=0.2 N,所以绳上的张力FT=0.2 N.设导体棒K中的电流为IK,则它所受安培力FK=B1IKl,对导体棒K,由平衡条件知FT=FK,所以电流IK=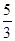 A.
A.
因为导体棒Q运动切割磁感线而产生电动势,相当于电源.等效电路如图所示,因K、S、Q相同,所以导体棒Q中的电流IQ=2IK=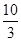 A
A

设导体棒Q运动的速度大小为v,则E=B2lv
由闭合电路的欧姆定律知IQ=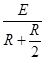
解得v=5 m/s
导体棒Q沿导轨向下匀速下滑过程中,受安培力FQ=B2IQl
由平衡条件知F+m1gsin 37°=FQ
代入数据解得F=0.4 N
所以Q杆所受拉力的瞬时功率
P=F·v=0.4×5 W=2 W.
点评:此题是电磁感应、运动学和能量的综合运用,考查同学们的综合分析解答能力,对学生的要求较高,此类题目属难度较大的压轴题,对于高考中能否得高分至关重要,在学习中需要多作练习.
