问题
选择题
物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零，则一个质量为m0的质点到质量为M0的引力源中心的距离为r0时，其万有引力势能为EP＝－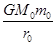
（式中G为万有引力常量）.一颗质量为m的人造地球卫星沿轨道半径为r1的圆形轨道环绕地球做匀速圆周运动，已知地球的质量为M，要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2，则卫星上的发动机所消耗的最小能量为：（假设卫星的质量始终不变，不计一切阻力及其它星体的影响）
A．E＝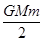
(
－
)
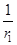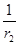B．E＝GMm(－)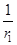
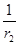C．E＝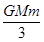
(－)
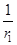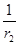D．E＝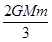
(－)
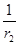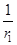答案
答案：A
题目分析：发动机所消耗的最小能量W等于卫星机械能的变化量，在轨道为r1 的轨道上，引力势能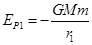
，根据万有引力提供向心力有
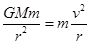可得动能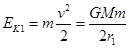
，同样道理在轨道为r2 的轨道上，有
，
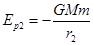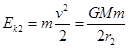，那么在变轨过程根据功能关系有
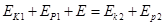，解得发动机消耗的最小能量
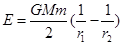对照选项A对。