如图所示,坐标系xOy位于竖直平面内,在该区域内有场强E="12" N/C、方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、沿水平方向且垂直于xOy平面指向纸里的匀强磁场.一个质量m=4×10-5 kg,电量q=2.5×10-5C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g="10" m/s2,求:

(1)P点到原点O的距离;
(2)带电微粒由原点O运动到P点的时间.
(1)15 m (2)1.2 s
微粒运动到O点之前要受到重力、电场力和洛伦兹力作用,在这段时间内微粒做匀速直线运动,说明三力合力为零.
由此可得
 ①
①
电场力FE=Eq ②
洛伦兹力FB=Bqv ③
联立求解、代入数据得v="10" m/s ④
微粒运动到O点之后,撤去磁场,微粒只受到重力、电场力作用,其合力为一恒力,且方向与微粒在O点的速度方向垂直,所以微粒在后一段时间内的运动为类平抛运动,可沿初速度方向和合力方向进行分解.
tanθ=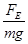 ⑤
⑤
代入数据得tanθ=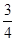 ⑥
⑥
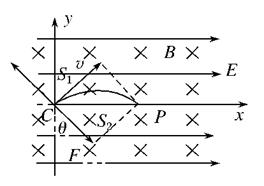
设沿初速度方向的位移为s1,沿合力方向的位移为s2,则因为
s1=vt ⑦
s2= t2 ⑧
t2 ⑧
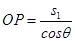 ⑨
⑨
联立求解,代入数据可得P点到原点O的距离
OP="15" m
O点到P点运动时间
t="1.2" s.
