如图所示,水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径 .在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度
.在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度 .现有一电荷量
.现有一电荷量 ,质量
,质量 的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取
的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取 .
.
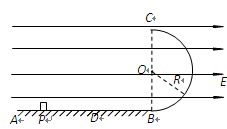
试求:
(1)带电体在圆形轨道C点的速度大小.
(2)D点到B点的距离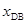 .
.
(3)带电体运动到圆形轨道B点时对圆形轨道的压力大小.
(4)带电体在从P开始运动到落至D点的过程中的最大动能。
(1) 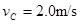 (2)
(2) 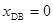 (3)
(3)  (4)
(4) 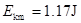
题目分析:(1)设带电体通过C点时的速度为vC,依据牛顿第二定律:
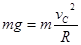 ---------------------------------1分
---------------------------------1分
解得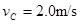 ------------------------------1分
------------------------------1分
(2)设带电体从最高点C落至水平轨道上的D点经历的时间为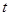 ,根据运动的分解有:
,根据运动的分解有:
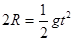 ------------------------------------1分
------------------------------------1分
 -----------------------------2分
-----------------------------2分
联立解得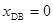 -------------------------------1分
-------------------------------1分
(3)设带电体通过B点时的速度为vB,设轨道对带电体的支持力大小为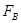 ,带电体在B点时,根据牛顿第二定律有
,带电体在B点时,根据牛顿第二定律有 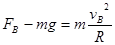 --------1分
--------1分
带电体从B运动到C的过程中,依据动能定理:
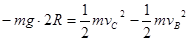 ---------------------------2分
---------------------------2分
联立解得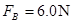 -------------------------------------1分
-------------------------------------1分
根据牛顿第三定律,带电体对轨道的压力 --------------1分
--------------1分
(4)由P到B带电体作加速运动,故最大速度一定出现在从B经C到D的过程中.在此过程中只有重力和电场力做功,这两个力大小相等,其合力与重力方向成45º夹角斜向右下方,故最大速度必出现在B点右侧对应圆心角为45 º处.
设小球的最大动能为 ,根据动能定理有:
,根据动能定理有:
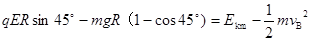 -----------2分
-----------2分
解得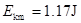 (或
(或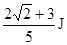 )--------------------1分
)--------------------1分
点评:做此类型的题目,需要根据圆周运动知识分析最高点或者最低点的速度,然后根据能量守恒定律分析解题
