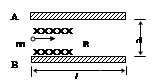
(10分)A、B为一平行板,板长为l,两板间距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里。一个质量为m,带电荷量 为+q的带电粒子以一定初速度沿A、B两板中线且垂直于磁感线方向射入磁场中,粒子恰好从A板的右边界飞出。粒子重力不计。求:
(1)粒子在磁场中运动的轨道半径r和射入磁场的初速度v0各是多少?
(2)粒子在磁场中运动的时间t是多少?
(1) v0=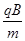 (
(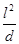 +
+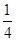 d) (2)t=
d) (2)t=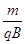 sin-1
sin-1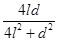
(1)设粒子做圆周运动的圆心为O(如图),
由几何条件可知:
r2=l2+(r- )2 ① 2分
)2 ① 2分
解之得r=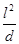 +
+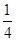 d 1分
d 1分
由牛顿第二定律可得:
qv0B=m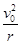 ②2分
②2分
解①、②式得v0=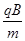 (
(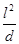 +
+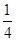 d) 1分
d) 1分
(2)设粒子从磁场飞出时,转过的圆心角为q,粒子做圆周运动的周期为T,则有
T=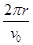 =
=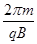 ③ 1分
③ 1分
tgq=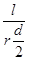 ④ 1分
④ 1分
t=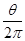 T ⑤ 1分
T ⑤ 1分
解①、③、④、⑤得t=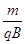 ×tg-1
×tg-1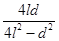 1分
1分
或t=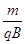 sin-1
sin-1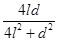
本题考查带电粒子在磁场中的运动,根据带电粒子在磁场中的偏转,先画出轨迹,找圆心,求半径,由洛伦兹力提供向心力求得粒子运动速度,求粒子的运动时间方法是:求出粒子偏转轨迹所对圆心,由周期公式和圆心的比例求得运动时间
