问题
计算题
宇航员在月球表面完成下面的实验：在一固定的竖直光滑圆轨道内部最低点静止一个质量为m的小球(可视为质点)，如图所示.当给小球一瞬间的速度v时，刚好能使小球在竖直平面内做完整的圆周运动，已知圆弧的轨道半径为r，月球的半径为R1，引力常量为G.求：
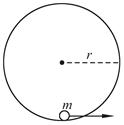
(1)若在月球表面上发射一颗环月卫星，所需最小发射速度为多大？
(2)轨道半径为2R1的环月卫星周期为多大？
答案
（1）
（2）4π
/v.
题目分析：（1）设月球表面的重力加速度为g1，小球在最高点的速度为v1，小球从最低点到最高点的过程中机械能守恒，有：
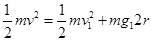（2 分）
小球刚好做完整的圆周运动，在最高点有：
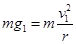（2 分）
由以上两式可得：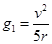
（1 分）
若在月球表面发射一颗环月卫星，则重力必须提供向心力，则有：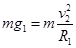
（1 分）
故最小发射速度：
v2=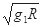
=
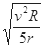=v
. 1 分
(2)若卫星在半径为2R1的轨道上，
GMm/(2R1)2=m·2R4π2/T2 2 分
其中g1=GM/R2=v2/5r
由以上几式可得：T=4π/v. 2 分