在如图甲所示的装置中,阴极K能够连续不断地发射初速不计的电子,这些电子经P、K间的电场加速后,都能通过P板上的小孔沿垂直于P板的方向进入P板右侧的区域,打到P板右侧L远处且与P平行的荧光屏Q上的O点,由于P、K相距很近,所有电子通过电场所用时间忽略不计。现在P与Q间加垂直纸面向里的匀强磁场,且从某一时刻t=0开始,在P、K间加一周期性变化的电压,电压随时间的变化关系如图乙所示,则从该时刻起,所有从小孔射出的电子恰好能全部打到荧光屏上。已知电子质量为m,带电量为e,粒子在磁场中做圆周运动的周期小于4T0,求:
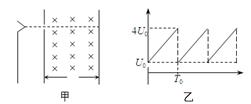
(1)电子打到荧光屏上的范围;
(2)从t=0时刻开始在电压变化的一个周期内,打到屏上距O点最近的电子与最远的电子的时间
(1) O点下方距O点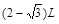 到L之间(2)
到L之间(2)
题目分析:(1)经U0加速的电子,在磁场中偏转半径最小,根据题意,刚好能与Q屏相切A点,设匀强磁场磁感应强度为B,即: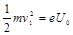 (1分)
(1分)
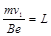 (1分)
(1分)
经最大电压加速的电子,在磁场中运动的轨道半径为R,与Q屏交于D点,则:
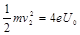 ,
, 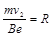 (2分)
(2分)
由以上各式及几何关系可算得,OA=L,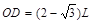 (2分)
(2分)
即电子打到荧光屏上的范围是O点下方距O点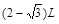 到L之间 (1分)
到L之间 (1分)
(2)设电子在磁场中运动周期为T,则: 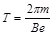 (1分)
(1分)
设经U0加速电压加速的电子离开电场后到达Q屏上的A点所用时间为t1,经4U0加速后的电子到达Q屏上的D点所用时间为t2,则: 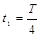 (1分)
(1分)
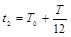 (1分)
(1分)
由以上各式可解得:  (2分)
(2分)
点评:该题涉及到带电粒子在电场和磁场的运动情况,对同学们的分析能力和数学功底要求较高,难度很大,属于难题.
