问题
计算题
如图所示,在平面直角坐标系xoy内,第I象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场。一质量为m、电荷量为q的带电粒子从电场中Q(-2h,-h)点以速度υ0水平向右射出,经坐标原点O处射入第I象限,最后以垂直于PN的方向射出磁场。已知MN平行于x轴, N点的坐标为(2h,2h),不计粒子的重力,求:

(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子磁场中运动的时间t.
答案
(1)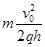 (2)
(2)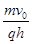 (3)
(3)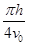
题目分析:(1)粒子在电场中做类平抛运动,由平抛运动规律及牛顿运动定律得
垂直电场线方向: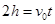
沿电场线方向: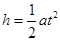
由牛顿第二定律得: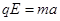
解得: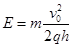
(2)粒子到达O点时,沿+y方向的分速度
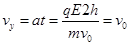
速度与x正方向的夹角a满足
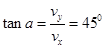
粒子从MP的中点垂直于MP进入磁场,垂直于NP射出磁场,
粒子在进场中的速度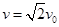
由几何关系知轨道半径 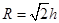
由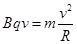 得
得
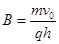
(3)粒子在磁场中的运动时间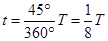
由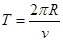 可得
可得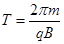
可得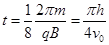
点评:带电粒子在组合场中的运动要注意分析过程,并结合各过程中涉及到的运动规律采用合理的物理规律求解。
