问题
计算题
(10分)如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2 kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1 kg、电荷量q=+0.2 C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6 N的恒力,g取10 m/s2,求:

(1)开始时木板和滑块的加速度分别是多少?
(2)木板的最大加速度为多少?
(3)滑块的最大速度为多少?
答案
(1)2 m/s2,2 m/s2 (2)3 m/s2 (3)10 m/s
题目分析:(1)根据整体法:开始滑块与板一起匀加速,刚发生相对滑动时整体的加速度
a=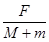 =2 m/s2
=2 m/s2
(2)对滑块受力分析可知μ(mg-qvB)=ma,则此刻v="6" m/s
由于在外力作用下加速,速度变大,因此此后滑块做加速度减小的加速运动,最终匀速.即mg=qvB
代入数据可得此时刻的速度为vmax="10" m/s.
(3)由于摩擦力随着速度增加而减小,所以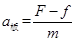 ,因此板做随加速度增加的,加速度变大的变加速运动,最终匀加速.
,因此板做随加速度增加的,加速度变大的变加速运动,最终匀加速.
所以板的最大加速度:a= =3 m/s2
=3 m/s2
点评:此类题型的关键在于对带电木块受力分析,通过左手定则可知其支持力在变小,因而得出摩擦力变小的规律,通过牛顿第二定律对物体受力分析便能得到稳定条件,从而解决问题。
