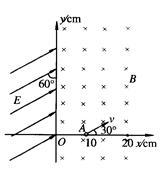
在如图所示的空间区域里,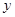 轴左方有一匀强电场,场强方向跟
轴左方有一匀强电场,场强方向跟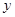 轴正方向成60°,大小为
轴正方向成60°,大小为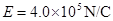 ;
;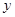 轴右方有一垂直纸面向里的匀强磁场,磁感应强度
轴右方有一垂直纸面向里的匀强磁场,磁感应强度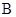 =0.20T.有一质子以速度
=0.20T.有一质子以速度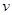 =2.0×
=2.0×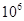 m/s,由
m/s,由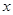 轴上的A点(10cm,0)沿与
轴上的A点(10cm,0)沿与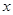 轴正方向成30°斜向上射入磁场,在磁场中运动一段时间后射入电场,后又回到磁场,经磁场作用后又射入电场.已知质子质量近似为
轴正方向成30°斜向上射入磁场,在磁场中运动一段时间后射入电场,后又回到磁场,经磁场作用后又射入电场.已知质子质量近似为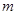 =1.6×
=1.6×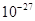 kg,电荷
kg,电荷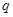 =1.6×
=1.6×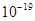 C,质子重力不计.求:
C,质子重力不计.求:
(1)质子在磁场中做圆周运动的半径.
(2)质子从开始运动到第二次到达y轴所经历的时间.(计算结果保留3位有效数字)
(3)质子第三次到达y轴的位置坐标.
(1)0.10m(2)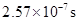 (3)(0,34.6cm)
(3)(0,34.6cm)
题目分析:(1)质子在磁场中受洛伦兹力做匀速圆周运动,
根据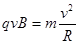 得:质子做匀速圆周运动的半径为
得:质子做匀速圆周运动的半径为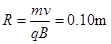
(2)由于质子的初速度方向与x轴正方向夹角为30°,且半径恰好等于OA,因此,质子将在磁场中做半个圆周到达y轴上的C点,如图所示.
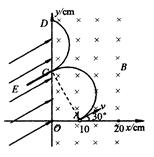
质子做圆周运动周期为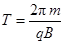 ,
,
质子从出发运动到第一次到达y轴的时间
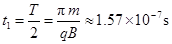 ,
,
质子进入电场时的速度方向与电场的方向相同,在电场中先做匀减速直线运动,速度减为零后反向做匀加速直线运动,设质子在电场中运动的时间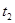 ,根据牛顿第二定律
,根据牛顿第二定律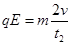 ,得
,得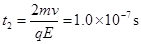 .
.
因此,质子从开始运动到第二次到达y轴的时间t为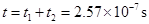 .
.
(3)质子再次进入磁场时,速度的方向与电场的方向相同,在洛伦兹力的作用下做匀速圆周运动,到达y轴的D点.
根据几何关系,可以得出C点到D点的距离为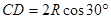 ;
;
则质子第二次到达y轴的位置为
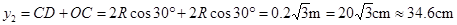 .
.
即质子第三次到达y轴的坐标为(0,34.6cm).
点评:分析带电粒子在磁场中运动,首先要画出粒子运动轨迹图,然后根据洛伦兹力做向心力可求半径,还可以根据几何关系求半径,找到粒子做圆周运动的圆心角可求出运动时间。如果还存在电场,粒子在电场中一般做匀变速直线运动或类平抛运动,类平抛运动要把运动分解后研究。
