问题
计算题
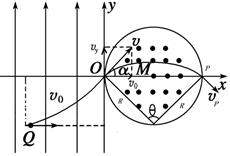
（12分）如图所示，在平面直角坐标系xOy内，第二、三象限内存在沿y轴正方向的匀强电场，第一、四象限内存在半径为L的圆形匀强磁场，磁场方向垂直于坐标平面向外。一个比荷（
）为K的带正电的粒子从第三象限中的Q(-2L，-L)点以速度v0沿x轴正方向射出，恰好从坐标原点O进入磁场，从P(2L，0)点射出磁场。不计粒子重力，求：
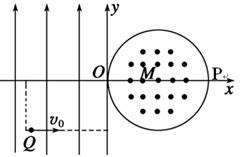
（1）电场强度E
（2）从P点射出时速度
的大小
（3）粒子在磁场与电场中运动时间之比
答案
（1）
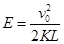（2）
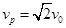（3）
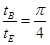
题目分析：（1）带电粒子在匀强电场中做类平抛运动，
加速度：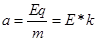
；
在电场中运动的时间：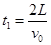
；
沿y轴正方向，则有：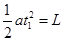
，
即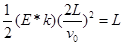
，则：；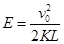
(2)带电粒子刚进入磁场时，沿y轴正方向的分速度
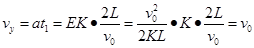
则带电粒子进入磁场时的速度
，
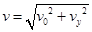
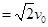由于在磁场中洛伦兹力不改变带电粒子速度大小，
则：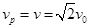
（3）由图可知，带电粒子进入磁场时，速度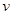
与x轴正方向夹角
，
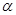满足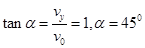
；
则偏转圆的圆心角
，
由几何关系可知，偏转半径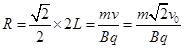
，则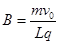
；
则粒子在磁场中运动时间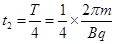
,即：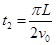
故：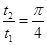
点评：此类题型的关键在于利用类平抛运动规律得出进入磁场的速度以及方向。通过左手定则判断粒子的洛伦兹力，画出轨迹，从而找到问题突破口。