问题
计算题
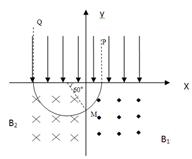
在xoy 平面第Ⅰ、Ⅱ象限中，存在沿y轴负方向的匀强电场，场强为E=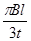
，在第Ⅲ、Ⅳ象限中,存在垂直于xoy平面方向如图所示的匀强磁场，磁感应强度B2 =" 2" B1 =" 2" B ，带电粒子a、b先后从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M(0,-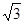
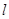)处发生正碰（即碰前两粒子速度方向相反），碰撞前带电粒子b的速度方向与y 轴正方向成60°角，不计粒子重力和两粒子间相互作用。求：
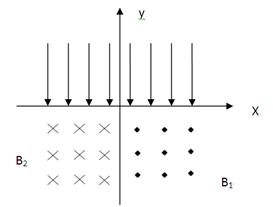
（1）两带电粒子的比荷及在磁场中运动的轨道半径；
（2）带电粒子释放的位置P、Q两点坐标及释放的时间差。
答案
（1）
、 
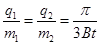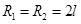
（2）P、Q两点的坐标分别为（l、2l）（-3l、8l） 时间差为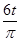
题目分析：（1）由题知a、b两带电粒子在M处发生正碰，其运动轨迹如图，由图可得：
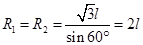
带电粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，进入磁场时的速度为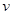
则
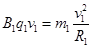，可得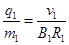
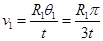
解得：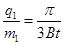
同理可得：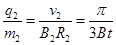
（2）由题可得：对P点释放的粒子有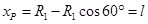
粒子由静止释放做匀加速直线运动，进入磁场时的速度为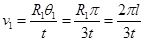
加速度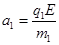
由匀变速直线运动规律得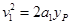
解得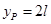
，则P点坐标为（l、2l）
同理
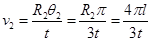
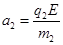
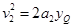
解得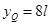
，则Q点坐标为（-3l、8l）
带电粒子释放的时间差为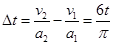
点评：本题关键是由带电粒子在M处发生正碰，画出粒子匀速圆周运动的轨迹，利用几何知识找出圆心及相应的半径。从而找到圆弧所对应的圆心角．由圆心和轨迹用几何知识确定半径是研究带电粒子在匀强磁场中做匀速圆周运动的重要方法．