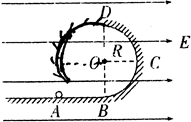
如图所示,ABCD为竖直放在场强为E=104V/m水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的圆形轨道,轨道的水平部分与其半圆相切,A为水平轨道上的一点,而且AB=R=0.2m,把一质量m=0.1kg、带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放,小球在轨道的内侧运动。(g取10m/s2)求:

(1)小球到达D点时对轨道压力是多大?
(2)若让小球安全通过轨道,开始释放点离B点至少多远?
(1)压力3N(2) x≥0.5 m
题目分析:到达D点时,由弹力和重力的合力提供向心力,只要求出D点速度就可以 (1)由A点到C点应用动能定理有:
Eq(AB+R)-mgR=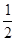 mvC2
mvC2
解得:vC=2 m/s
在C点应用牛顿第二定律得:
FN-Eq=m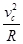
得FN=3 N
由牛顿第三定律知,小球在C点对轨道的压力为3 N.
(2)小球要安全通过D点,必有mg≤m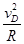 .
.
设释放点距B点的距离为x,由动能定理得:
Eqx-mg·2R=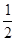 mvD2
mvD2
以上两式联立可得:x≥0.5 m
点评:在本题中物体不仅受重力的作用,还有电场力,在解题的过程中,一定要分析清楚物体的受力和运动过程,根据动能定理和牛顿第二定律灵活列式求解.
