f（x）=x³-2x=x（x²-2）=0∴x=-

2

或0或

2

∵f（-x）=-f（x），∴f（x）为奇函数．

∀0＜x₁＜x₂f（x₁）-f（x₂）=（x₁-x₂）（x₁²+x₁x₂+x₂²-2）＞（x₁-x₂）（3x₁²-2）

当x＞

2 3

=

6

3

时，f（x₁）-f（x₂）＞0，f（x）单调递增．

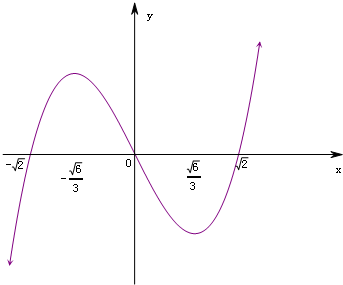
由对称性画出草图n∈[a-1，a+1]

∵1＜

2 6

3

＜2，

∴m∈[a-1，a+1]，f（n）为n∈[a-1，a+1]时的值域的长度d．要使f（n）的值域最小当a-1＜-

6

3

＜

6

3

＜a+1时f（n）的值域最小，则d=f(-

6

3

)-f(

6

3

)=

8

9

6

S=2d=

16

9

6

，

故答案为

16

9

6

．