如图所示，倾角为37°的光滑绝缘的斜面上放着M=1kg的U型导轨abcd，ab∥cd。另有一质量m=1kg的金属棒EF平行bc放在导轨上，EF下侧有绝缘的垂直于斜面的立柱P、S、Q挡住EF使之不下滑。以OO′为界，下部有一垂直于斜面向下的匀强磁场，上部有平行于斜面向下的匀强磁场。两磁场的磁感应强度均为B=1T，导轨bc段长L=1m。金属棒EF的电阻R=1.2Ω，其余电阻不计。金属棒与导轨间的动摩擦因数μ=0.4，开始时导轨bc边用细线系在立柱S上，导轨和斜面足够长。当剪断细线后，试求：
（1）细线剪短瞬间，导轨abcd运动的加速度；
（2）导轨abcd运动的最大速度；
（3）若导轨从开始运动到最大速度的过程中，流过金属棒EF的电量q=5C，则在此过程中，系统损失的机械能是多少？（sin37°=0.6）
（1）a=2.8m/s2（2）vm=5.6m/s（3）20.32J
题目分析：（1）线剪断瞬间，对导轨用牛顿第二定律：
（2分）
其中 
解得：a=2.8m/s2。 （1分）
（2）对导轨下滑过程用牛顿第二定律：
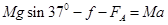（2分）
把
及
代入得：
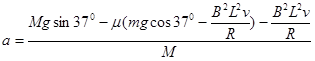
=gsin37°-
μgcos37°-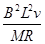
(1-μ)
令上式a=0，得导轨的最大速度为：
vm=5.6m/s （3分）
（3）设导轨下滑距离d时达到最大速度，则有：
q=I△t=
="BLd/R" （2分）
解得： d=6m （1分）
对系统用能量守恒定律得：
（2分）
代入数据解得：
=20.32J （1分）
点评：本题难度中等，线框下滑过程中，当受力平衡时速度最大，由受力分析可求得最大速度，由公式q=I△t可推导求解流过导体横截面的电量，对导线框，重力势能的减小转化为动能和焦耳热
