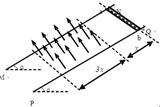
(14分)如图所示,两根足够长的平行光滑金属导轨MN、PQ与水平面的夹角为a=30°,导轨电阻不计,导轨处在垂直导轨平面斜向上的有界匀强磁场中. 两根电阻都为R=2W、质量都为m=0.2kg的完全相同的细金属棒ab和cd垂直导轨并排靠紧的放置在导轨上,与磁场上边界距离为x=1.6m,有界匀强磁场宽度为3x=4.8m.先将金属棒ab由静止释放,金属棒ab刚进入磁场就恰好做匀速运动,此时立即由静止释放金属棒cd,金属棒cd在出磁场前已做匀速运动.两金属棒在下滑过程中与导轨接触始终良好(取重力加速度g=10m/s2).求:
(1)金属棒ab刚进入磁场时棒中电流I;
(2)金属棒cd在磁场中运动的过程中通过回路某一截面的电量q;
(3)两根金属棒全部通过磁场的过程中回路产生的焦耳热Q.
(1) I=1A (2)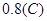 (3) 8J
(3) 8J
题目分析:(1)mgxsina=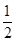 mv12, v1=
mv12, v1=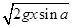 =4m/s(1分)
=4m/s(1分)
 =mgsina,BL=1Tm(1分)
=mgsina,BL=1Tm(1分)
BIL=mgsina,I=1A (1分)
(2)设经过时间t1,金属棒cd也进入磁场,其速度也为v1,金属棒cd在磁场外有x=v1/2·t1,此时金属棒ab在磁场中的运动距离为:X=v1t1=2x,
两棒都在磁场中时速度相同,无电流,金属棒cd在磁场中而金属棒ab已在磁场外时,cd棒中才有电流,运动距离为2x(得到cd棒单独在磁场中运动距离为2x,即可得2分)
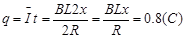 (公式2分、结果1分)
(公式2分、结果1分)
(3)金属棒ab在磁场中(金属棒cd在磁场外)回路产生的焦耳热为:
Q1=mgsina´2x=3.2J (或:Q1=2I2Rt1=mgsina´2x)(1分)
金属棒ab、金属棒cd都在磁场中运动时,回路不产生焦耳热。两棒加速度均为gsina,ab离开磁场时速度为v 2,v22-v12=2gxsina,v2= 。(1分)
。(1分)
金属棒cd在磁场中(金属棒ab在磁场外),金属棒cd的初速度为v2= ,末速度为
,末速度为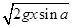 ,由动能定理:
,由动能定理:
mgsina´2x-Q2=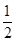 m(
m(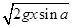 )2-
)2-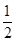 m(
m( )2(2分)
)2(2分)
Q2=mgsina´3x=4.8J(1分)
Q=mgsina´5x=8J(1分)
点评:在分析导体棒切割磁感线运动问题时,需要结合受力分析, 特别是把握好题目的临界条件,比如什么时候匀速运动,
