问题
计算题
(14分)如图所示,足够长的间距为L=0.2m光滑水平导轨EM、FN与PM、QN相连,PM、QN是两根半径为d=0.4m的光滑的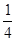 圆弧导轨,O、P连线水平,M、N与E、F在同一水平高度,水平和圆弧导轨电阻不计,在其上端连有一阻值为R=8W的电阻,在PQ左侧有处于竖直向上的有界匀强磁场,磁感应强度大小为B0=6T。现有一根长度稍大于L、质量为m=0.2kg、电阻为r=2W的金属棒从轨道的顶端P处由静止开始下滑,到达轨道底端MN时对轨道的压力为2mg,取g=10m/s2,求:
圆弧导轨,O、P连线水平,M、N与E、F在同一水平高度,水平和圆弧导轨电阻不计,在其上端连有一阻值为R=8W的电阻,在PQ左侧有处于竖直向上的有界匀强磁场,磁感应强度大小为B0=6T。现有一根长度稍大于L、质量为m=0.2kg、电阻为r=2W的金属棒从轨道的顶端P处由静止开始下滑,到达轨道底端MN时对轨道的压力为2mg,取g=10m/s2,求:

(1)棒到达最低点MN时金属棒两端的电压;
(2)棒下滑到MN过程中金属棒产生的热量;
(3)从棒进入EM、FN水平轨道后开始计时,磁场随时间发生变化,恰好使棒做匀速直线运动,求磁感应强度B随时间变化的表达式。
答案
(1)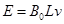 ;(2)0.08J;(3)
;(2)0.08J;(3)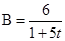
题目分析:在导轨最低点MN处,
由牛顿第二定律得: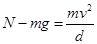 且N=2mg 2分
且N=2mg 2分
解得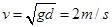 1分
1分
金属棒产生的电动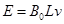 1分
1分
金属棒两端的电压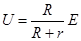 1分
1分
联立得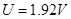 1分
1分
(2)由能量守恒(功能关系)得: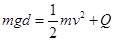 2分
2分
金属棒产生的热量: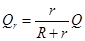 1分
1分
联立得:Qr="0.08J" 1分
(3) 因为棒做匀速直线运动,故棒和电阻R组成的回路磁通量不变
在t=0时刻,回路磁通量Ф0=B0Ld 2分
在t时刻,回路磁通量Ф=BL(d+vt) 1分
由Ф0=Ф可得 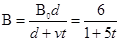 1分
1分
