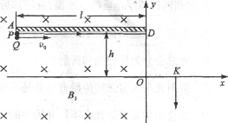
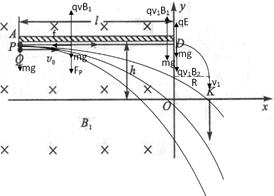
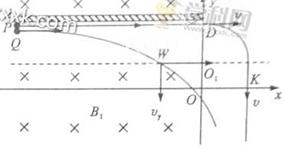
如下图所示，竖直平面（纸面）内有直角坐标系xOy，x轴沿水平方向。在x≤O的区域内存在方向垂直于纸面向里，磁感应强度大小为B1的匀强磁场。在第二象限紧贴y轴固定放置长为l、表面粗糙的不带电绝缘平板，平板平行于x轴且与x轴相距h。在第一象限内的某区域存在方向相互垂直的匀强磁场（磁感应强度大小为B2、方向垂直于纸面向外）和匀强电场（图中未画出）。一质量为m、不带电的小球Q从平板下侧A点沿x轴正向抛出；另一质量也为m、带电量为q的小球P从A点紧贴平板沿x轴正向运动，变为匀速运动后从y轴上的D点进入电磁场区域做匀速圆周运动，经
圆周离开电磁场区域，沿y轴负方向运动，然后从x轴上的K点进入第四象限。小球P、Q相遇在第四象限的某一点，且竖直方向速度相同。设运动过程中小球P电量不变，小球P和Q始终在纸面内运动且均看作质点，重力加速度为g。求：
（1）匀强电场的场强大小，并判断P球所带电荷的正负；
（2）小球Q的抛出速度v0的取值范围；
（3）B1是B2的多少倍？
（1）E=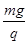
P球带正电 （2）0＜v0＜
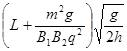（3）
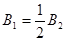
根据题意，受力分析如图所示。
（1）根据题述条件，带电小球P在电磁复合场中做匀速圆周运动，必有重力与电场力平衡，设所求匀强电场的场强大小为E，有mg=qE ①
即E=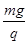 ②
小球P紧贴平板运动，其所受洛伦兹力必竖直向上，根据左手定则可知，小球P带正电。
（2）设小球P紧贴平板匀速运动的速度为v，此时洛伦兹力与重力平衡，有B1qv=mg ③
设小球P以速度v在电磁场区域内做圆周运动的半径为R，有B2qv=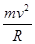
④
设小球Q和小球P在第四象限相遇点的坐标为（x，y），有x=R，y＜0 ⑤
设小球Q运动到相遇点的时间为t0，水平方向的位移为s，竖直方向的位移为d，有
s=v0t0 ⑥
d=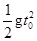
⑦
由题意得，x=s-l，y=h-d ⑧
联立各方程，由题意可知，v0大于0，得0＜v0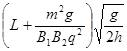＜ ⑨
（3）小球Q做平抛运动，要满足题设要求，则运动到小球P穿出磁场区域时的同一水平高度时的W点时，其竖直方向的速度vy和竖直位移yQ必修满足
vy=v ⑩
yQ=R （11）
设小球Q运动到W点的时间为t，由平抛运动，有
vy=gt ⑩
yQ=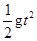
（11）
联立相关方程，解得。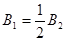
【考点定位】带电小球在混合场中的运动、平抛运动、匀速圆周运动。