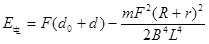如图所示,光滑平行的水平金属导轨MNPQ相距L,在M点和P点间接一个阻值为R
的电阻,在两导轨间矩形区域内有垂直导轨平面竖直向下、宽为d的匀强磁场,磁感应强度为B.一质量为m,电阻为r的导体棒ab,垂直搁在导轨上,与磁场左边界相距d0.现用一大小为F、水平向右的恒力拉ab棒,使它由静止开始运动,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的接触,导轨电阻不计).求:
(1)在图中标出当棒ab进入磁场后流过电阻R的电流方向;
(2)棒ab在离开磁场右边界时的速度;
(3)棒ab通过磁场区的过程中整个回路所消耗的电能.
(1) 由右手定则可判断流过电阻R的电流从M到P;
(2) 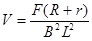 ;
;
(3) 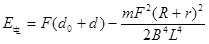 。
。
题目分析:导体棒进入磁场,切割磁感线产生感应电流,使得导体棒受到安培力作用,导体棒在磁场中做匀速运动时,其所受的外力F和安培力平衡,据此可以求出棒的速度.根据动能定理(或能量守恒定律)可以求出电路中消耗的电能,注意克服安培力所做功等于整个回路中产生的电能.
解答过程:(1)ab进入磁场后,由右手定则可判断流过电阻R的电流从M到P。
(2)设ab棒离开磁场右边界前做匀速运动的速度为V,则产生的感应电动势为:
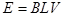 (1)
(1)
由闭合电路欧姆定律得,回路中的电流为:
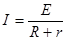 (2)
(2)
对ab棒,由平衡条件得:
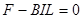 (3)
(3)
联立(1)、(2)、(3)式解得:
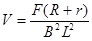 (4)
(4)
(3) 从ab棒开始运动到离开磁场右边界,由动能定理得
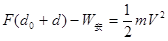 (5)
(5)
克服安培力做的功等于电路中产生的电能,则
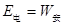 (6)
(6)
由(4)、(5)、(6)式解得
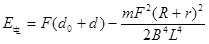 (7)
(7)
故ab棒通过磁场区的过程中整个回路所消耗的电能为: