问题
计算题
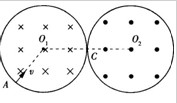
如右图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度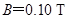 ,磁场区域半径
,磁场区域半径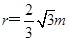 ,左侧区圆心为
,左侧区圆心为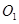 ,磁场向里,右侧区圆心为
,磁场向里,右侧区圆心为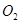 ,磁场向外.两区域切点为C.今有质量
,磁场向外.两区域切点为C.今有质量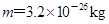 .带电荷量
.带电荷量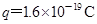 的某种离子,从左侧区边缘的A点以速度
的某种离子,从左侧区边缘的A点以速度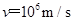 正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
(1)该离子通过两磁场区域所用的时间.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为多大?(侧移距离指垂直初速度方向上移动的距离)
答案
(1) 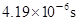 (2)2 m
(2)2 m
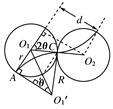
题目分析:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,如右图,设轨迹半径为R,圆周运动的周期为T.
由牛顿第二定律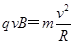 ①
①
又 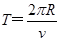 ②
②
联立①②得: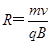 ③
③
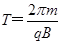 ④
④
将已知代入③得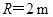 ⑤
⑤
由轨迹图知: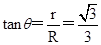 ,则
,则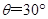
则全段轨迹运动时间:
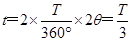
联立④⑥并代入已知得:
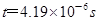
(2)在图中过O2向AO1作垂线,联立轨迹对称关系侧移总距离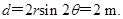
点评:本题是有界磁场问题,关键是画出粒子的运动轨迹,运用几何知识求解半径.
