问题
计算题
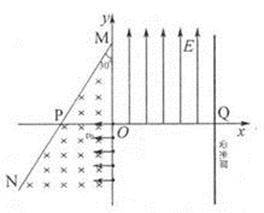
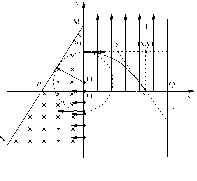
如图所示,在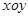 平面直角坐标系中,直线
平面直角坐标系中,直线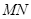 与
与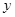 轴成30°角,
轴成30°角, 点的坐标为(
点的坐标为(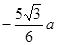 ,0),在
,0),在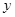 轴与直线
轴与直线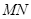 之间的区域内,存在垂直于
之间的区域内,存在垂直于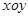 平面向里磁感强度为
平面向里磁感强度为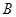 的匀强磁场.均匀分布的电子束以相同的速度
的匀强磁场.均匀分布的电子束以相同的速度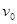 从
从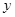 轴上
轴上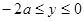 的区间垂直于
的区间垂直于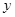 轴和磁场方向射入磁场.己知从
轴和磁场方向射入磁场.己知从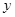 轴上
轴上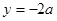 点射入磁场的电子在磁场中的轨迹恰好经过
点射入磁场的电子在磁场中的轨迹恰好经过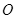 点,忽略电子间的相互作用,不计电子的重力.
点,忽略电子间的相互作用,不计电子的重力.
(1)电子的比荷( );
);
(2)有一电子,经过直线MP飞出磁场时,它的速度方向平行于y轴,求该电子在y轴上的何处进入磁场;(3)若在直角坐标系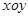 的第一象限区域内,加上方向沿
的第一象限区域内,加上方向沿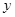 轴正方向大小为
轴正方向大小为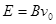 的匀强电场,在
的匀强电场,在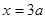 处垂直于
处垂直于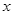 轴放置一平面荧光屏,与
轴放置一平面荧光屏,与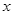 轴交点为
轴交点为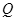 ,求:从O点上方最远处进入电场的粒子打在荧光屏上的位置。
,求:从O点上方最远处进入电场的粒子打在荧光屏上的位置。
答案
(1)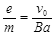 (2)
(2)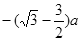 (3)
(3)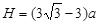
题目分析:(1)由题意可知电子在磁场中的半径为a
由: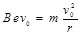 电子的比荷:
电子的比荷: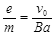
(2)设该电子射入的纵坐标为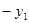
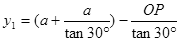 解得
解得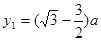
该电子在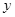 轴上进入磁场的纵坐标为:
轴上进入磁场的纵坐标为: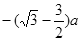
(3)粒子能进入电场中,且离O点上方最远,则粒子在磁场中运动圆轨迹必须与直线MN相切,粒子轨道的圆心为O′点。
则: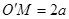
由三角函数关系可求得: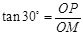 ; 得:
; 得: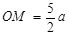
有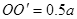 即粒子垂直于
即粒子垂直于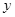 轴进入电场的位置离O点上方最远距离为
轴进入电场的位置离O点上方最远距离为 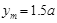
电子在电场中做类平抛,设电子在电场的运动时间为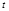 ,竖直方向位移为
,竖直方向位移为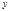 ,水平位移为
,水平位移为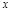 ,
,
水平方向: 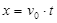 竖直方向:
竖直方向: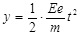
代入得: 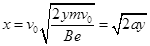
设电子最终打在光屏的最远点距Q点为H,电子射出电场时的夹角为θ有:
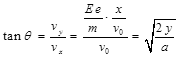
有: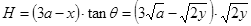
将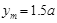 代入可得,打在荧光屏上的位置为距离Q点
代入可得,打在荧光屏上的位置为距离Q点