问题
计算题
(18分)有一个1000匝的矩形线圈,两端通过导线与平行金属板AB相连(如图所示),线圈中有垂直纸面向外的匀强磁场;已知AB板长为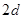 ,板间距离为
,板间距离为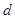 。当穿过线圈的磁通量增大且变化率为
。当穿过线圈的磁通量增大且变化率为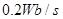 时,有一比荷为
时,有一比荷为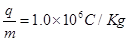 的带正电粒子以初速度
的带正电粒子以初速度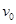 从上板的边缘射入板间,并恰好从下板的边缘射出;之后沿直线MN运动,又从N点射入另一垂直纸面向外磁感应强度为
从上板的边缘射入板间,并恰好从下板的边缘射出;之后沿直线MN运动,又从N点射入另一垂直纸面向外磁感应强度为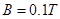 的圆形匀强磁场区(图中未画出),离开圆形磁场时速度方向偏转了
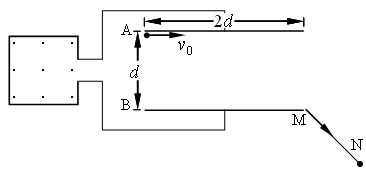
的圆形匀强磁场区(图中未画出),离开圆形磁场时速度方向偏转了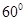 。不计带电粒子的重力。试求
。不计带电粒子的重力。试求
(1)AB板间的电压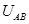
(2)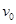 的大小
的大小
(3)圆形磁场区域的最小半径
答案
(1)200V;(2)2×104m/s;(3)0.14m。
题目分析:(1)由法拉第电磁咸应定律: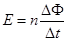 ①
①
得矩形线圈产生的感应电动势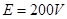 ②
②
因为AB板间的电压等于线圈产生的电动势,故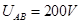 ③
③
(2)由于带电粒子在AB板间做类平抛运动,设从下板边缘离开时竖直方向的速度为 ,
,
则极板间的电场强度为E=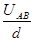 ,粒子受到的电场力为F=Eq=
,粒子受到的电场力为F=Eq= ,
,
则粒子在竖直方向的加速度为: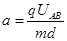 ④
④
水平方向: ⑤
⑤
竖直方向: ⑥
⑥
由④⑤⑥并代入数据得: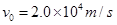 ⑦ (其它方法求解依照给分)
⑦ (其它方法求解依照给分)
(3)粒子进入磁场瞬间: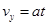
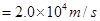 ⑧
⑧
带电粒子在圆形磁场区中做匀速圆周运动,
洛伦兹力作向心力: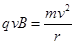 ⑨
⑨
粒子进入磁场的速度为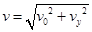 ⑩
⑩
由⑧⑨⑩并代入数据得: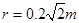 11
11
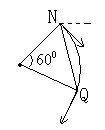
如图,由几何关系得弦NQ的长为: 12
12
在过NQ两点的圆中,以弦NQ为直径的圆最小,
圆形磁场区域的最小半径为: 13
13
评分标准:①③④⑨13每式2分,其余每式1分。
