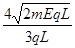问题
计算题
(16分)如图所示，在xoy平面内，y轴左侧有沿x轴正方向的匀强电场，电场强度大小为E；在0＜x＜L区域内，x轴上、下方有相反方向的匀强电场，电场强度大小均为2E；在x＞L的区域内有垂直于xoy平面的匀强磁场，磁感应强度大小不变、方向做周期性变化。一电荷量为q、质量为m的带正电粒子(粒子重力不计)，由坐标为(－L，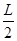
)的A点静止释放。
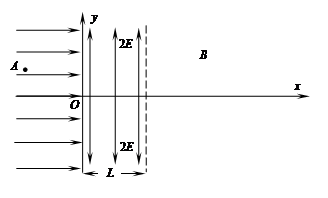
⑴求粒子第一次通过y轴时速度大小；
⑵求粒子第一次射入磁场时的位置坐标及速度；
⑶现控制磁场方向的变化周期和释放粒子的时刻，实现粒子能沿一定轨道做往复运动，求磁场的磁感应强度B大小取值范围。
答案
⑴v0＝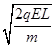
；⑵(L，L)，v＝
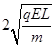，方向与x轴正方向成45°角斜向上；⑶0＜B＜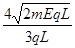
题目分析：⑴粒子在y轴左侧的匀强电场中被加速做直线运动，根据动能定理有：qEL＝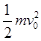
－0
解得粒子第一次通过y轴时速度大小为：v0＝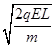
⑵粒子进入偏转电场后作类平抛运动，设其运动时间为t，在x方向上有：L＝v0t
在y方向上有：Δ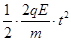y＝
，vy＝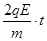
解得：Δy＝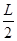
，vy＝v0
所以粒子第一次射入磁场时的位置坐标为(L，L)
速度大小为：v＝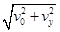
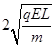＝，方向与x轴正方向成45°角斜向上
⑶在磁场中，粒子做匀速圆周运动，根据向心力公式和牛顿第二定律有：qvB＝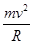
解得粒子做匀速圆周运动的轨道半径为：R＝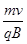
由对称性可知，射出磁场后必须在x轴下方的电场中运动，才能实现粒子沿一定轨道做往复运动，如图所示。
当CC1＝＋＋＝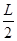
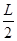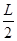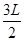时，轨道半径R最小，对应的磁感应强度B最大，粒子紧贴x轴进入y轴左侧的电场
根据图中几何关系有：R2＋R2＝CC12
解得最小半径为：R＝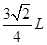
，对应的磁感应强度的最大值为：Bmax＝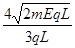
所以磁感应强度大小取值范围：0＜B＜