问题
计算题
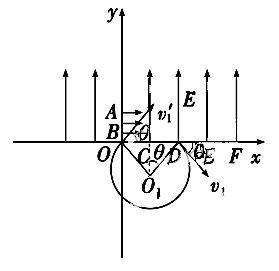
如图所示，在xOy坐标系中，y>0的范围内存在着沿y轴正方向的匀强电场；在y<0的范围内存在着垂直纸面的匀强磁场(方向未画出)。已知OA＝OC＝CD＝DE＝EF＝L，OB＝
L。现在一群质量为m、电荷量大小为q(重力不计)的带电粒子，分布在A、B之间。t＝0时刻，这群带电粒子以相同的初速度v0沿x轴正方向开始运动。观察到从A点出发的带电粒子恰好从D点第一次进入磁场，然后从O点第一次离开磁场。
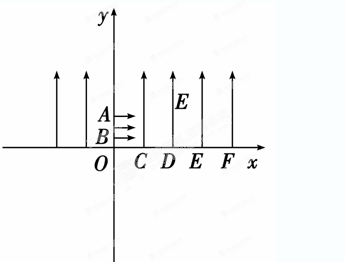
(1)试判断带电粒子所带电荷的正负及所加匀强磁场的方向；
(2)试推导带电粒子第一次进入磁场的位置坐标x与出发点的位置坐标y的关系式；
(3)试求从A点出发的带电粒子，从O点第一次离开磁场时的速度方向与x轴正方向的夹角θ。(图中未画出)
答案
（1）负电 匀强磁场方向沿垂直纸面向里 （2）x＝2
（3）45°
题目分析：(1)由带电粒子在电场中的偏转方向可知：该带电粒子带负电；
根据带电粒子在磁场中做圆周运动的情况，由左手定则知匀强磁场方向沿垂直纸面向里。
(2)设带电粒子在电场中的加速度为a，对于从A点进入电场的粒子，有：
L＝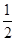
at
①
2L＝v0t1 ②
由①②式解得a＝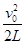
③
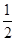y＝at2 ④
x＝v0t ⑤
由④⑤式解得：x＝2 ⑥
从位置坐标y出发的带电粒子，从x位置坐标离开电场
(3)由几何知识可得：θ与带电粒子第一次进入磁场时与x轴正方向的夹角相等。对于从A点进入电场的带电粒子，其y轴方向的速度：
vy1＝at1 ⑦
tanθ＝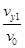
⑧
由⑦⑧式解得：tanθ＝1，所以θ＝45°