问题
计算题
（15分）．如图所示，在空间中取直角坐标系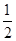
，在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，MN为电场的理想边界，场强大小为E1 ，ON="d" 。在第二象限内充满一个沿x轴负方向的匀强电场，场强大小为E2。电子从y轴上的A点以初速度
沿x轴负方向射入第二象限区域，它到达的最右端为图中的B点，之后返回第一象限，且从MN上的P点离开。已知A点坐标为（0，h）．电子的电量为e，质量为m，电子的重力忽略不计，求：
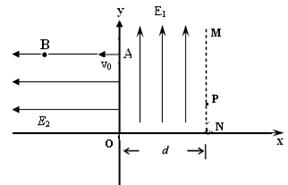
（1）电子从A点到B点所用的时间
（2）P点的坐标；
（3）电子经过x轴时离坐标原点O的距离．
答案
（1）
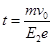（2）
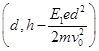（3）
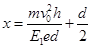
题目分析：（1）从A到B的过程中，
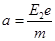
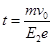
（2）电子从A运动到B，然后沿原路返回到A点时的速度大小仍是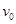
电子在电场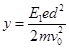
中的运动时间为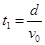
偏转加速度为：
电子的偏转位移为：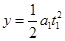
联立解得：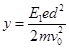
P点的坐标为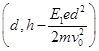
（3）电子到达P点时
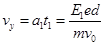（1分）
电子离开电场后水平、竖直方向上都做匀速运动，
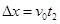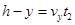（1分）
（1分）
电子经过x轴是离坐标原点O的距离为：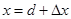
联立解得：