问题
解答题
已知A、B、C是直线l上的不同的三点,O是直线外一点,向量
(1)求函数y=f(x)的解析式; (2)若x∈[
(3)若关于x的方程f(x)=2x+b在[0,1]上恰有两个不同的实根,求实数b的取值范围. |
答案
(1)由题意,
=(OA
x2+1)•3 2
+[ln(2+3x)-y]•OB OC
∵A、B、C三点共线,
∴
x2+1+ln(2+3x)-y=13 2
∴y=
x2+ln(2+3x)3 2
(2)∵x∈[
,1 6
],a>ln1 3
,则a>lnx1 3
又由(1)得,f/(x)=
+3x,x∈[3 2+3x
,1 6
],则f/(x)-3x=1 3
>03 2+3x
∴要证原不等式成立,只须证:a>lnx+ln
(*)3 2+3x
设h(x)=lnx+ln
=ln3 2+3x
.3x 2+3x
∵h/(x)=
•2+3x 3x
=3(2+3x)-3x•3 (2+3x)2
>02 x(2+3x)
∴h(x)在x∈[
,1 6
]上均单调递增,则h(x)有最大值h(1 3
)=ln1 3
,1 3
又因为a>ln
,所以a>h(x)在x∈[1 3
,1 6
]恒成立.1 3
∴不等式(*)成立,即原不等式成立.
(3)方程f(x)=2x+b即
x2-2x+ln(2+3x)=b,令ϕ(x)=3 2
x2-2x+ln(2+3x),3 2
∴ϕ/(x)=
+3x-2=3 2+3x
=9x2-1 2+3x (3x+1)(3x-1) 2+3x
当x∈(0,
)时,ϕ′(x)<0,ϕ(x)单调递减,1 3
当x∈(
,1)时,ϕ′(x)>0,ϕ(x)单调递增,1 3
∴ϕ(x)有极小值为ϕ(
)=ln3-1 3
即在[0,1]上的最小值.1 2
又ϕ(0)=ln2,ϕ(1)=ln5-
,又ln5-1 2
-ln2=ln1 2
=5 2 e
ln1 2
>25 4e
ln1 2
>025 4×3
∴ln5-
>ln2.1 2
∴要使原方程在[0,1]上恰有两个不同实根,必须使ln3-
<b≤ln2.1 2

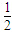 mgtgθ
mgtgθ mgsinθ
mgsinθ