问题
计算题
（17分）如图所示，在xoy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场E1，第二象限存在水平向右的匀强电场E2（未知），其它区域存在垂直于坐标平面向外的匀强磁场。有一质量为m、电量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场垂直x轴进入偏转电场E2，过y轴正半轴上的P点再次进入匀强电场E1，已知OP=h，不计粒子重力，求：
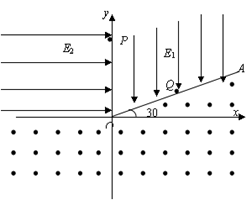
(1)粒子经过Q点时的速度大小；
(2)匀强电场电场强度E1的大小；
(3)粒子从Q点运动到P点所用的时间。
答案
（1）2V0 （2）
（3）
＋
题目分析：（1）设粒子在Q的速度为V，则V·sin30°=V0 有V=2V0
（2）在电场E1中，对粒子有h－OQ·sin30°=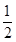
at2 OQ·cos30°=V0t
粒子的加速度qE1=ma V·cos30°=a·t 得：E1= OQ=
h
（3）粒子以O为圆心作匀速圆周运动OQ=" r" =
T=
在磁场中运动时间t1=
·T=
在电场E2中运动时间t2=
=
Q点运动到P点的时间t=t1＋t2=＋