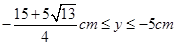问题
计算题
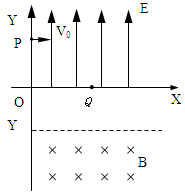
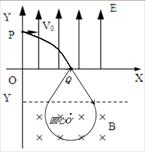
(18分)如图所示,在 平面内的第一象限内存在沿
平面内的第一象限内存在沿 轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度
轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度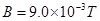 ,有一质量为
,有一质量为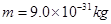 ,电量为
,电量为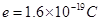 的电子以
的电子以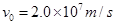 的速度从
的速度从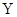 轴的
轴的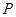 点(0,
点(0,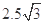 cm)沿
cm)沿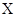 轴正方向射入第一象限,偏转后从
轴正方向射入第一象限,偏转后从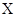 轴的
轴的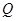 点射入第四象限,方向与
点射入第四象限,方向与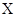 轴成
轴成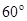 角,在磁场中偏转后又回到
角,在磁场中偏转后又回到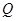 点,方向与
点,方向与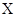 轴也成
轴也成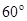 角;不计电子重力.求:
角;不计电子重力.求:
(1)OQ之间的距离及电子通过Q点的速度大小.
(2)若在第四象限内的磁场的边界为直线边界,即在虚线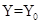 的下方有磁场,如图中所示,求
的下方有磁场,如图中所示,求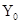 的坐标.
的坐标.
(3)若在第四象限内的磁场为圆形边界的磁场,圆形边界的磁场的圆心坐标的范围.
答案
(1)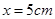 ,
,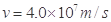 (2)
(2)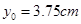 (3)
(3)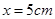 ,
,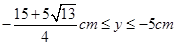
题目分析:(1)电子在电场做类平抛运动,从P到Q过程中,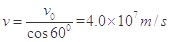 ①
①
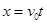 ②
② 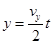 ③
③ 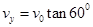 ④
④
解得: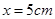 ⑤
⑤
(2)电子在磁场中做匀速圆周运动,故有: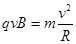 ⑥
⑥
由几何关系可知,电子回到Q点有: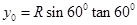 ⑦
⑦
解得: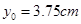 ⑧
⑧
(3)由于在磁场中偏转后又回到Q点,方向与X轴也成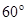 角.其运动轨迹如图:
角.其运动轨迹如图:
由几何关系可知,圆形磁场的圆心在Q点的正下方,即: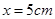
圆形磁场应与电子轨迹有公共弦,同时只要磁场半径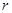 大于
大于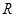 即可,故磁场圆心y轴的最小坐标为:
即可,故磁场圆心y轴的最小坐标为:
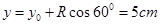
圆形磁场在第四象限,磁场半径应小于5cm,由几何关系可知,磁场圆心y轴的最大坐标为:
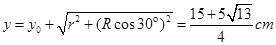
即圆形磁场的圆心的坐标应满足: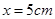 ,
,