问题
解答题
将边长为a的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
答案
设小正方形的边长为x,则盒底的边长为a-2x,
由于a-2x也要>0,则x∈(0,
),a 2
且方盒是以边长为a-2x的正方形作底面,高为x的正方体,
其体积为V=x(a-2x)2,(x∈(0,
))a 2
V'=(a-2x)(a-6x),令V'=0,则x1=
,x2=a 2
,a 6
由x1=
∉(0,a 2
),且对于x∈(0,a 2
),V′>0,x∈(a 6
,a 6
),V′<0,a 2
∴函数V在点x=
处取得极大值,由于问题的最大值存在,a 6
∴V(
)=a 6
即为容积的最大值,此时小正方形的边长为2a3 27
.a 6

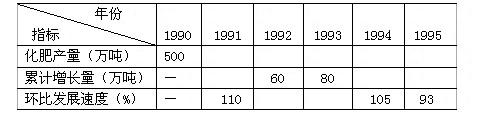 要求:(结果保留2位小数,写出公式,计算过程及结果)
要求:(结果保留2位小数,写出公式,计算过程及结果)