问题
填空题
已知函数f(x)=
|
答案
求导函数可得:
+2e2 (ex+1)2
>0恒成立,故f(x)在区间[-k,k](k>0)上单调增.1 1+x2
所以有:M=f(x)max=f(k),m=f(x)min=f(-k)
∴M+m=f(k)+f(-k)=
+ln(k+3ek+1 ek+1
)+1+k2
+ln(-k+3e-k+1 e-k+1
)1+k2
=
+ln(k+3ek+1 ek+1
)+1+k2
+ln(-k+3+ek ek+1
)1+k2
=4+ln(1+k2-k2)=4+ln(1)=4+0=4
故答案为:4

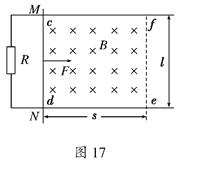
 x,且棒在运动到ef处时恰好静止,则外力F作用的时间为多少?
x,且棒在运动到ef处时恰好静止,则外力F作用的时间为多少?