问题
填空题
已知函数f(x)=ax3-3x+1对x∈(0,1]总有f(x)≥0成立.则实数a的取值范围是______.
答案
当x∈(0,1]时,不等式ax3-3x+1≥0可化为a≥
,3x-1 x3
设g(x)=
,x∈(0,1],3x-1 x3
g′(x)=
=-3x3-(3x-1)×3x2 x6
,6(x-
)1 2 x4
g′(x)与g(x)随x变化情况如下:
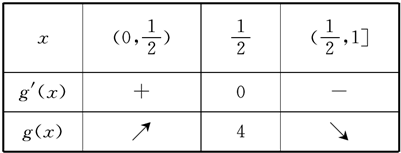
因此g(x)的最大值为4,则实数a的取值范围是[4,+∞).
故答案为:[4,+∞)
