(1)当a=-4时,f(x)=-4lnx+x2,函数的定义域为(0,+∞).
f′(x)=-+2x=.
当x∈[1,)时,f′(x)0,
所以函数f(x)在[1,)上为减函数,在(,e]上为增函数,
由f(1)=-4ln1+12=1,f(e)=-4lne+e2=e2-4,
所以函数f(x)在[1,e]上的最大值为e2-4,相应的x值为e;
(2)由f(x)=alnx+x2,得f′(x)=+2x=.
若a≥0,则在[1,e]上f′(x)>0,函数f(x)=alnx+x2在[1,e]上为增函数,
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若a<0,由f′(x)=0,得x=-(舍),或x=.
若≤1,即-2≤a<0,f(x)=alnx+x2在[1,e]上为增函数,
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若≥e,即a≤-2e2,f(x)=alnx+x2在[1,e]上为减函数,
由f(1)=1,f(e)=alne+e2=e2+a≤-e2<0,
所以方程f(x)=0在[1,e]上有1个实数根;
若1<<e,即-2e2<a<-2,
f(x)在[1,]上为减函数,在[,e]上为增函数,
由f(1)=1>0,f(e)=e2+a.
f(x)min=f()=ln(-)-=[ln(-)-1].
当-<e,即-2e<a<-2时,f()>0,方程f(x)=0在[1,e]上的根的个数是0.
当a=-2e时,方程f(x)=0在[1,e]上的根的个数是1.
当-e2≤a<-2e时,f()<0,f(e)=a+e2≥0,方程f(x)=0在[1,e]上的根的个数是2.
当-2e2<a<-e2时,f()<0,f(e)=a+e2<0,方程f(x)=0在[1,e]上的根的个数是1;
(3)若a>0,由(2)知函数f(x)=alnx+x2在[1,e]上为增函数,
不妨设x1<x2,则|f(x1)-f(x2)|≤|-|变为f(x2)+<f(x1)+,由此说明函数G(x)=f(x)+在[1,e]单调递减,所以G′(x)=+2x-≤0对x∈[1,e]恒成立,即a≤-2x2+对x∈[1,e]恒成立,
而-2x2+在[1,e]单调递减,所以a≤-2e2+.
所以,满足a>0,且对任意的x1,x2∈[1,e],都有|f(x1)-f(x2)|≤|-|成立的实数a的取值范围不存在.

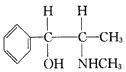 它可能具有的化学性质为 [ ]
它可能具有的化学性质为 [ ]