问题
解答题
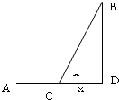
有甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的两侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为3a元和5a元,问供水站C建在何处才能使水管费用最省?
答案
据题意知,只有点C在线段AD上某一适当位置,才能使总运费最省,
设C点距D点xkm,如图所示,则BD=40,AC=50-x,
∴BC=
=BD2+CD2
又设总的水管费用为y元,402+x2
由题意得y=3a(50-x)+5a
(0<x<50),x2+402
y′=-3a+
令y′=0解得x=30.5ax x2+402
在(0,50)上,y只有一个极值点,
根据实际意义,函数在x=30(km)处取得最小值,
此时AC=50-x=20(km),
答:供水站C建立在A、D之间距甲厂20km处,可使水管费用最省.