（1）求函数f（x）=x³-6x+5的导数，得f'（x）=3（x²-2），

令f'（x）=0，即3（x²-2）=0，解得x1=-

2

，x2=

2

，

列表讨论f′（x）的符号，得

x	(-∞，- 2 )	- 2	(- 2 ， 2 )	2	( 2 ，+∞)
f'（x）	+	0	-	0	+
f（x）	↗	极大值	↘	极小值	↗

∴f（x）的单调递增区间是(-∞，-

2

)，(

2

，+∞)，单调递减区间是(-

2

，

2

)，

当x=-

2

时，函数有极大值为5+4

2

，当x=

2

时，函数有极小值为5-4

2

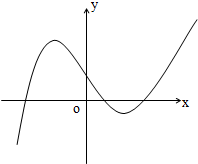
（2）由（1）的分析可知y=f（x）图象的大致形状及走向如图：

若关于x的方程f（x）=a有3个不同实根，即y=f（x）图象与直线y=a有3个不同交点，

由图数形结合可得

5-4

2

＜a＜5+4

2

（3）f（x）≥k（x-1）即（x-1）（x²+x-5）≥k（x-1）．

∵x＞1，∴k≤x²+x-5在（1，+∞）上恒成立，

令g(x)=x2+x-5=(x+

1

2

)2-

21

4

，则g（x）在（1，+∞）上是增函数，

∴g（x）＞g（1）=-3，

∴k≤-3．