问题
解答题
已知函f(x)=x3+ax2+bx+5,若x=
(1)求函数f(x)的解析式; (2)求y=f(x)在[-4,1]上的最大值和最小值. (3)函数y=f(x)-m有三个零点,求实数m的取值范围. |
答案
(1)f′(x)=3x2+2ax+b,…(1分)
由题意,得
,解得f′(
)=3×(2 3
)2+2a×2 3
+b=02 3 f′(1)=3×12+2a×1+b=3
;a=2 b=-4
所以,f(x)=x3+2x2-4x+5,…(4分)
(2)由(1)知f(x)=3x3+4x-4=(x+2)(3x-2),
令f′(x)=0,得x1=-2,x2=
;…(5分)2 3
| x | -4 | (-4,-2) | -2 | (-2,
|
| (
| 1 | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||||
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ | ||||||||
| 函数值 | -11 | 13 |
| 4 |
∴f(x)在[-4,-1]上的最大值为13,最小值为-11.…(9分)
(3)∵函数y=f(x)-m有三个零点,即f(x)=m,有三个交点,
可得f(x)的图象:如下图:
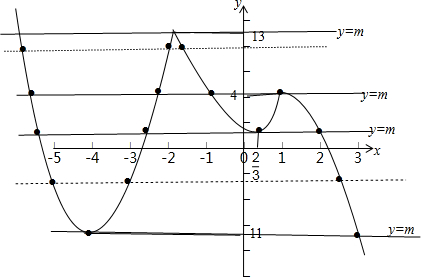
由上图y=m与函数f(x)有三个交点,
∴4<m<13,-11<m<
,此时y=m与f(x)交于三点;95 27
∴4<m<13 或-11<m<
;95 27
