参考答案：C

解析： 麦考利久期(Macaulay Duration)，又叫麦考利持续期，是考虑了债券所包含的现金流因素后的到期日，也即债券各期现金流量的加权平均年份，或债券的加权平均到期期限。麦考利久期的计算公式为：

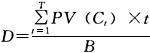其中，B为债券的当前市场价格，

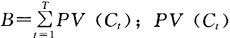是债券未来第t期的利息现金流量折现值，T是利息流量发生的期间总数。 零息债券即到期一次性还本付息的债券。根据定义，零息债券的麦考利久期为：

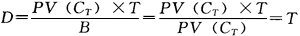可见，零息债券的麦考利久期就等于它的名义到期期限。 关于麦考利久期有以下几个结论： 定理一：贴现债券的麦考利久期等于它的名义到期时间。所谓贴现债券就是打折出售，到期偿还面额的债券。其现金流量发生的方式与零息债券相同，所以其麦考利久期的性质也与零息债券相同。 定理二：附息债券(即定期支付利息，到期还本的债券)的麦考利久期小于或等于它们的到期时间。这不难理解，因为加权平均数不会大于其中最大的那个被平均的数字。在麦考利久期的计算公式中，这个最大的被平均数字就是债券的名义到期期间数T。 其中，只有仅剩最后一期就要期满的附息债券的麦考利久期才等于它们的到期时间。因为这个时候的附息债券仅就现金流量发生的特点来看，与贴现债券或零息债券完全相同。 定理三：统一公债的麦考利久期等于(1+1/r)，其中r是计算现金流量现值所采用的贴现率。 统一公债为英国特有，它的期限无穷长。也就是说，在发行这种债券的时候，英国政府并没有规定到期的期限。当特定条件获得满足的时候，英国政府可以赎回。 我们令C为统一公债每期支付的利息，则该债券的市场价值为：

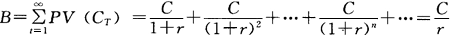该统一公债的麦考利久期为：

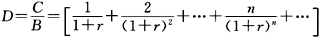进而有： 在上式两边同乘以(1+r)，有：

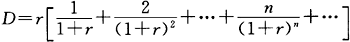然后将上述两个式子相减，得：

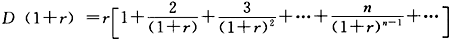从而有： 由以上分析可知，A的久期为5年，B的久期小于等于5年，C的久期为10年，D的久期小于等于10年。所以，本题应选C。