参考答案：C

解析：
生产者需要根据市场的需求状况及其成本水平来决定自己的最优生产规模，以确保企业的效益达到最优。在假定市场需求状况及其价格不变的前提下，企业经营的目标就是促使自己的平均生产成本在每一个产量水平上都能达到最低。
长期平均成本属于规划的范畴，自然应该是相应产量水平下的最低平均成本。短期平均成本则是某个具体规划付诸实施以后所达成的实际结果。纯按理论来说，一个产量水平对应一个生产规划，而一个生产规划对应着一个最低(从而最优)的(长期)平均成本水平。
每个最低(长期)平均成本水平的实现就会形成一个相应的短期成本函数，但这个短期成本函数也只是在相应的那个产量水平上才能满足长期平均成本最低的要求。在其他的产量水平上，该短期成本函数并不满足长期平均成本最低的要求。
另外，这个满足长期平均成本最低的点也不一定就是该短期平均成本曲线的最低点。因为该短期平均成本曲线最低点所代表的产量水平只是在现有企业(固定成本)规模下的最低成本产量水平。实际上，在该产量水平下很可能存在另外一个企业(固定成本)规模，在这个企业(固定成本)规模下，该产量水平上的短期平均成本更低。
因此，纯按理论来说，短期平均成本曲线有无数个，而长期平均成本曲线就是与无数个短期平均成本曲线相切的那些切点的轨迹，即长期平均成本曲线(LAC)是短期平均成本曲线(SAC)的包络线，或叫做计划线。
例如，考虑这样一种简单的生产过程：某企业使用两种可变投入(数量分别为x₁和x₂)和一种固定投入(数量为k)生产一种产品(产量为Q)。假定其生产函数为Q=f(x₁，x₂，k)，其中的k也可以被理解为用于刻画企业规模的参数。其成本函数为C=r₁x₁+r₂x₂+(k)，其中的C为总成本水平，r₁和r₂分别为两种可变投入(既定)的价格，(k)为与特定生产规模相应的固定成本水平，且

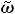_k(k)＞0。再假定等产量线与等成本线切点(厂商均衡点)的轨迹，即生产规模(均衡)扩张途径的函数形式为g(r₁，r₂，x₁，x₂，k)=0。
则由g(r₁，r₂，x₁，x₂，k)=0和Q=f(x₁，x₂，k)联立方程组，消掉x₁和x₂，进而将成本函数调整成C=(Q，k)-

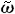(k)的形式。显然，每给定一个k，由这个成本函数就可以得出一个相应的短期成本函数的具体形式。
将短期成本函数C=

(Q，k)+

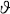(k)写成隐函数的形式：
C-

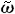(Q，k)-

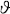(k)=G(C，Q，k)=0
且令其关于k的偏导数等于零，则从下列方程组中消掉k，就能得到长期成本函数：
C=φ(Q)

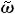
而LAC=C/Q=φ(Q)/Q
一般来说，随着企业生产规模的扩大，企业的规模报酬通常依次出现递增、不变、然后递减的过程。与之相应的，企业的长期平均成本曲线呈“U”字型的形态，即随着生产量的增加，长期平均成本先递减后递增。
在假定资本存量(即固定总成本)一定的前提下，根据边际产量递减的规律，随着产量的增大，短期平均成本也呈“U”字型的形态。因此，长期平均成本曲线与短期平均成本曲线之间的几何关系如下图所示：

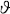
不难理解，除了SAC₂曲线外，LAC曲线不可能在任意SAC曲线的最低点处与之相切。实际上，当LAC曲线呈下降状态时，它与SAC曲线的切点应该在相应SAC曲线最低点的左侧(如SAC₁)；当LAC曲线呈上升状态时，它与SAC曲线的切点应该在SAC曲线最低点的右侧(如SAC₃)；只有在LAC曲线的最低点位置，它才会与SAC₂曲线在其最低点处相切。
所以，本题应选择C。