问题
解答题
已知函数f(x)=x2+xsinx+cosx.
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(a,f(a))处与直线y=b相切,求a与b的值.
答案
(1)由f(x)=x2+xsinx+cosx,
得f′(x)=2x+sinx+xcosx-sinx=x(2+cosx).
令f′(x)=0,得x=0.
列表如下:
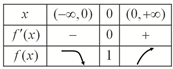
∴函数f(x)在区间(-∞,0)上单调递减,
在区间(0,+∞)上单调递增,
∴f(0)=1是f(x)的最小值;
(2)∵曲线y=f(x)在点(a,f(a))处与直线y=b相切,
∴f′(a)=a(2+cosa)=0,b=f(a),
解得a=0,b=f(0)=1.
