问题
证明题
设函数f(x)=ax2+blnx，其中ab≠0，证明：当ab＞0时，函数f(x)没有极值点；当ab＜0时，函数f(x)有且只有一个极值点，并求出极值．
答案
证明：因为f(x)=ax2+blnx，ab≠0，所以f(x)的定义域为(0，+∞)，
，
当ab＞0时，如果a＞0，b＞0，f′(x)＞0，f(x)在(0，+∞)上单调递增；
如果a＜0，b＜0，f′(x)＜0，f(x)在(0，+∞)上单调递减，
所以当ab＞0时，函数f(x)没有极值点；
当ab＜0时，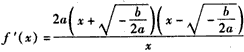
，
令f′(x)=0，得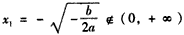
（舍去），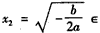
(0，+∞)，
当a＞0，b＜0时，f′(x)、f(x)随x的变化情况如下表：
从上表可看出，函数f(x)有且只有一个极小值点，极小值为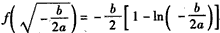
；
当a＜0，b＞0时，f′(x)、f(x)随x的变化情况如下表：
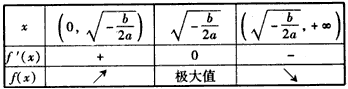
从上表可看出，函数f(x)有且只有一个极大值点，极大值为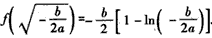
；
综上所述，当ab＞0时，函数f(x)没有极值点；
当ab＜0时，若a＞0，b＜0时，函数f(x)有且只有一个极小值点，极小值为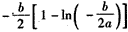
；
若a＜0，b＞0时，函数f(x)有且只有一个极大值点，极大值为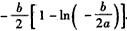
。