问题
解答题
已知函数f（x）=x3+ax2-（2a+3）x+a2（a∈R）。
（1）若函数f（x）在区间（1，+∞）上有极小值点，求实数a的取值范围；
（2）若当x∈[-1，1]时，f（x）>0，求实数a的取值范围。
答案
解：（1）)f '（x）= 3x2+2ax-（2a+3）=（3x+2a+3）（x-1），
令f'（x）=0，得x=1或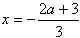
使函数f（x）在区间（1，+∞）上有极小值点，则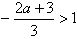
解得a＜-3；
（2）由题意知，x∈[-1，1]时，f（x）min>0
①当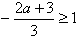
时，即a≤-3时f（x）在x∈[ -1，1]上单调递增，
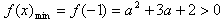
得a>-1或a<-2，由此得：a≤-3；
②当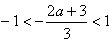
时，即-3＜a＜0，f（x）在
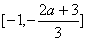上为增函数，
在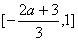
上为减函数，所以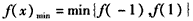
得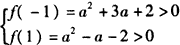
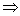a＞2或a＜-2
由此得-3＜a＜-2；
③当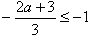
时，即a≥0，f（x）在x∈[-1，1]上为减函数，
所以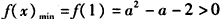
得a>2或a＜-1
由此得a＞2
由①②③得实数a的取值范围为a>2或a<-2。