问题
解答题
设函数f(x)=(x-a)2lnx，a∈R，
（Ⅰ）若x=e为y=f(x)的极值点，求实数a；
（Ⅱ）求实数a的取值范围，使得对任意的x∈(0，3e]，恒有f(x)≤4e2成立。
注：e为自然对数的底数。
答案
（Ⅰ）解：求导得f′(x)=2(x-a)lnx+
，
因为x=e是f(x)的极值点，
所以f'(e)=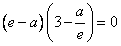
，
解得a=e 或a=3e，经检验，符合题意，
所以a=e或a=3e。
（Ⅱ）解：①当0＜x≤1时，对于任意的实数a，恒有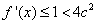
成立；
②当1＜x≤3e，由题意，首先有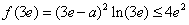
，
解得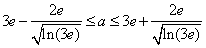
；
由（Ⅰ）知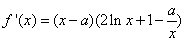
，
，
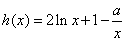则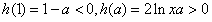
，
且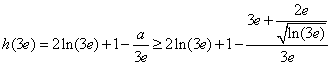
，
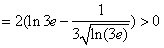又h(x)在（0，+∞）内单调递增，
所以函数h(x)在（0，+∞）内有唯一零点，记此零点为x0，
则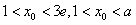
，
从而，当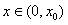
时，
；当
时，
；当
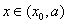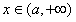时，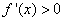
，
即f(x)在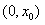
内单调递增，在
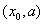内单调递减，在
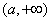内单调递增；
所以要使f(x)≤4e2对x∈(1，3e]恒成立，
只要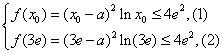
成立，
，知
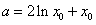，（3）
将（3）代入（1）得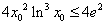
，
又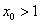
，注意到函数
在[1，+∞)内单调递增，故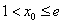
；
再由（3）以及函数2xlnx+x在（1，+∞)内单调递增，可得
。
由（2）解得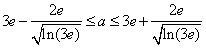
，
所以
；
综上，a的取值范围为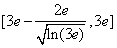
。