问题
解答题
已知函数f（x）=x3+ax+2在x=1时取得极值，
（Ⅰ）求a的值；
（Ⅱ）求函数f（x）在x=2处的切线方程。
答案
解：（Ⅰ）由已知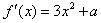
，且f′（1）=0，
得a=-3；
（Ⅱ）由（Ⅰ）得f′（2）=9，f（2）=4，
∴切点坐标为（2，4），切线斜率为9，
∴f（x）在x=2处的切线方程为y=9x-14。
搜题请搜索小程序“爱下问搜题”
已知函数f（x）=x3+ax+2在x=1时取得极值，
（Ⅰ）求a的值；
（Ⅱ）求函数f（x）在x=2处的切线方程。
解：（Ⅰ）由已知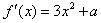，且f′（1）=0，
得a=-3；
（Ⅱ）由（Ⅰ）得f′（2）=9，f（2）=4，
∴切点坐标为（2，4），切线斜率为9，
∴f（x）在x=2处的切线方程为y=9x-14。