问题
解答题
已知函数f(x)=(x3-6x2+3x+t)ex,t∈R。
(Ⅰ)若函数y=f(x)依次在x=a,x=b,x=c(a<b<c)处取极值,求t的取值范围;
(Ⅱ)若存在实数t∈[0,2],使对任意的x∈[1,m],不等式f(x)≤x恒成立,求正整数m的最大值。
答案
解:(Ⅰ)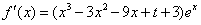 ,
,
∵f(x)有三个极值点,
∴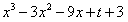 有三个根a、b、c,
有三个根a、b、c,
令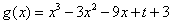 ,则
,则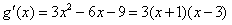 ,
,
∴g(x)在(-∞,-1),(3,+∞)上递增,在(-1,3)上递减,
∵g(x)有三个零点,
∴g(-1) >0,g(3) <0,
∴-8<t<24,
即t的取值范围是(-8,24)。
(Ⅱ)不等式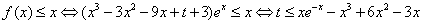 ,
,
转化为存在实数t∈[0,2],使对任意的x∈[1,m],不等式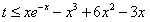 恒成立,
恒成立,
即不等式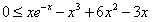 在x∈[1,m]上恒成立。
在x∈[1,m]上恒成立。
设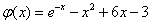 ,则
,则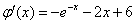 ,
,
设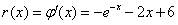 ,则
,则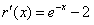 ,
,
∵x∈[1,m],∴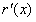 <0,
<0,
故r(x)在区间1,m]上是减函数,
又r(1)=4-e-1>0,r(2)=2-e-2>0,r(3)=-e-3<0,
故存在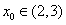 ,使得
,使得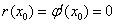 ;
;
当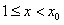 时有
时有 ,当
,当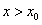 时有
时有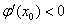 ;
;
从而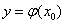 在区间[1,
在区间[1,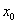 ]上递增,在区间[
]上递增,在区间[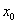 ,+∞)上递减,
,+∞)上递减,
又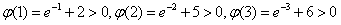 ,
,
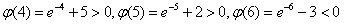 ,
,
∴当1≤x≤5时,恒ψ(x)>0有;当x≥6时,恒有ψ(x)<0,
故使命题成立的正整数m的最大值为5。
