问题
解答题
已知x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)当直线y=b与函数y=f(x)的图像有3个交点,求b的取值范围.
答案
解:(Ⅰ)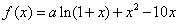 ,
,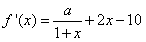 ,
,
x=3是函数 的一个极值点,
的一个极值点,
∴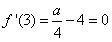 ,∴a=16;
,∴a=16;
(Ⅱ)由(Ⅰ)知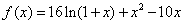 ,x∈(-1,+∞),
,x∈(-1,+∞),
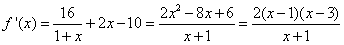 ,
,
令f′(x)=0,得x=1,x=3,
f′(x)和f(x)随x的变化情况如下:

∴f(x)的增区间是(-1,1),(3,+∞);减区间是(1,3)。
(Ⅲ)由(Ⅱ)知,f(x)在(-1,1)上单调递增,在(3,+∞)上单调递增,在(1,3)上单调递减, ∴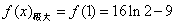 ,
, ,
,
又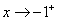 时,f(x)→-∞;x→+∞时,f(x)→+∞;
时,f(x)→-∞;x→+∞时,f(x)→+∞;
可据此画出函数y=f(x)的草图(图略),
由图可知,当直线y=b与函数y=f(x)的图像有3个交点时,b的取值范围为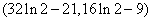 .
.
