问题
解答题
已知f(x)=ax-lnx,x∈(0,e],a∈R。
(1)若a=1,求f(x)的极小值;
(2)是否存在实数a,使f(x)的最小值为3。
答案
解:(1)∵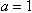
∴
令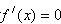 ,则
,则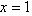
列表得:
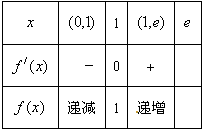
f(x)的极小值是1.
(2)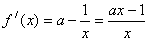
当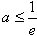 时,
时,
所以f(x)在(e, )单调递减,则f(x)的最小值为
)单调递减,则f(x)的最小值为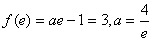 ,舍去
,舍去
当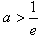 时,
时,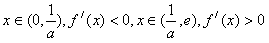
则f(x)的最小值为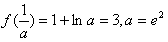
综上,当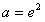 时,f(x)的最小值为3。
时,f(x)的最小值为3。
已知f(x)=ax-lnx,x∈(0,e],a∈R。
(1)若a=1,求f(x)的极小值;
(2)是否存在实数a,使f(x)的最小值为3。
解:(1)∵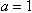
∴
令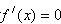 ,则
,则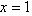
列表得:

f(x)的极小值是1.
(2)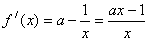
当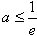 时,
时,
所以f(x)在(e, )单调递减,则f(x)的最小值为
)单调递减,则f(x)的最小值为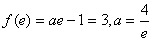 ,舍去
,舍去
当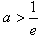 时,
时,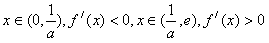
则f(x)的最小值为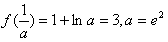
综上,当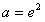 时,f(x)的最小值为3。
时,f(x)的最小值为3。