问题
解答题
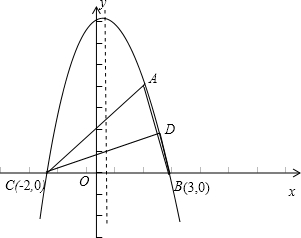
已知二次函数y=ax2+bx+c的图象经过A(2,4),其顶点的横坐标是
(1)此函数的解析式,并画出图象; (2)在x轴上方的图象上是否存在着D,使S△ABC=2S△DBC?若存在,求出D的值;若不存在,说明理由. |
答案
(1)∵二次函数y=ax2+bx+c的图象经过A(2,4),
∴4a+2b+c=4 ①
∵顶点的横坐标是
,1 2
-
=b 2a
②1 2
∵函数图象与x轴交点为B(x1,0)和(x2,0),
∴x1+x2=-
,x1x2=b a
,c a
∴x12+x22=(x1+x2)2-2x1x2=
=13③b2-2ac a2
x12+x22=(x1+x2)2-2x1x2,
由②得:a=-b代入①得:-2b+c=4 c=2b+4,
将a=-b c=2b+4代入③得:b2+2b(2b+4)=13b2,
b=0或b=1
∵b=0不合题意,
∴b=1,a=-1,c=6
∴y=-x2+x+6;
(2)设D(x,y) 则S△ABC=
×BC×4=10,1 2
S△DBC=
×5|y|=1 2
y=5,5 2
∴y=2,
将y=2代入y=-x2+x+6,
x=1± 17 2
∴D(
,2)或(1+ 17 2
,2).1- 17 2